Memahami Bangun Datar: Latihan Soal Kelas 1 SMP
Matematika seringkali dianggap sebagai mata pelajaran yang menantang, namun dengan pemahaman konsep yang kuat dan latihan yang memadai, segala kerumitan dapat diatasi. Salah satu topik fundamental dalam matematika di tingkat Sekolah Menengah Pertama (SMP), khususnya kelas 1, adalah mengenai bangun datar. Memahami sifat-sifat bangun datar, cara menghitung luas dan kelilingnya, serta mengidentifikasi hubungan antar bangun datar adalah pondasi penting untuk pembelajaran matematika di jenjang selanjutnya. Artikel ini akan membahas secara mendalam mengenai contoh-contoh soal bangun datar yang relevan untuk siswa kelas 1 SMP, disertai dengan penjelasan langkah demi langkah untuk membantu pemahaman.
Apa Itu Bangun Datar?
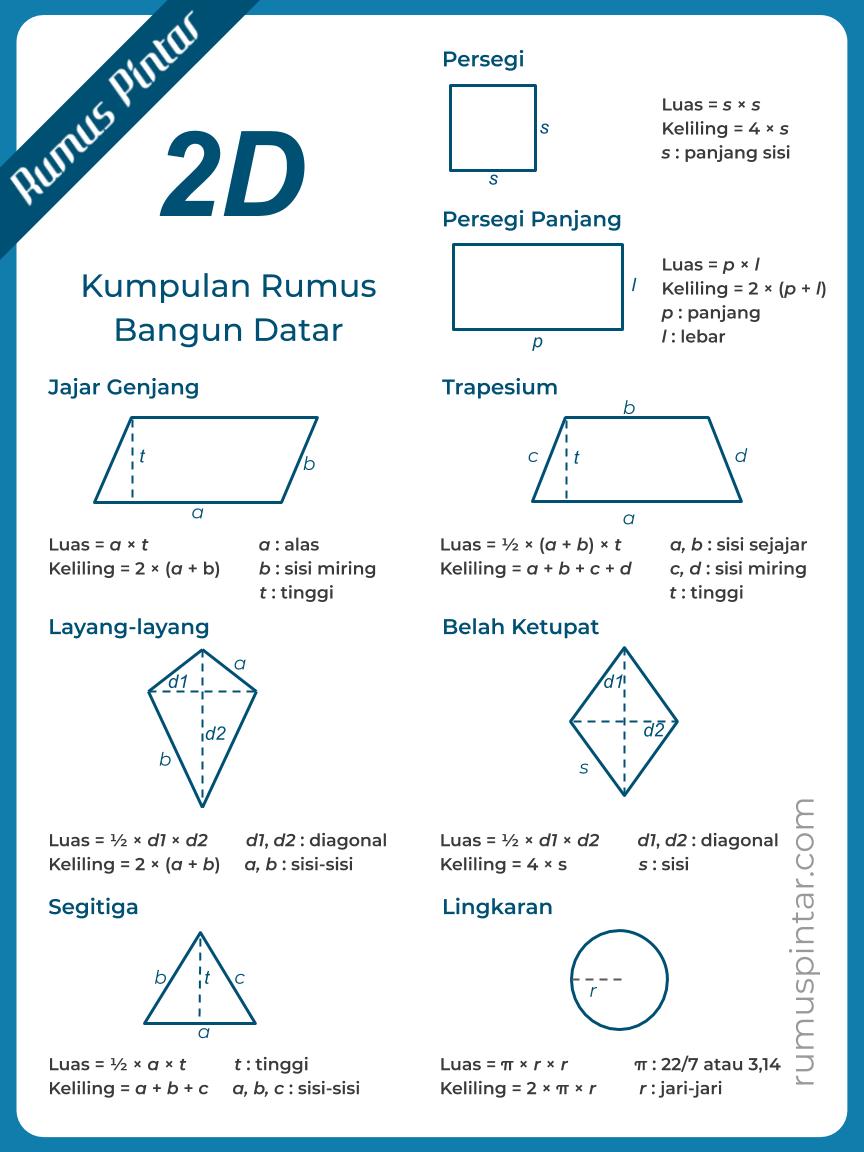
Sebelum masuk ke contoh soal, mari kita definisikan terlebih dahulu apa yang dimaksud dengan bangun datar. Bangun datar adalah bangun dua dimensi yang memiliki panjang dan lebar, tetapi tidak memiliki kedalaman atau ketebalan. Bangun datar hanya dapat digambarkan pada bidang datar. Contoh bangun datar yang umum kita temui antara lain persegi, persegi panjang, segitiga, lingkaran, jajargenjang, trapesium, dan belah ketupat.
Pentingnya Memahami Bangun Datar
- Dasar Geometri: Bangun datar adalah blok bangunan dasar dari geometri. Memahaminya membuka jalan untuk mempelajari bangun ruang dan konsep geometri yang lebih kompleks.
- Aplikasi Nyata: Konsep bangun datar banyak diaplikasikan dalam kehidupan sehari-hari, mulai dari desain arsitektur, seni, hingga perhitungan material dalam konstruksi.
- Kemampuan Berpikir Logis: Menyelesaikan soal-soal bangun datar melatih kemampuan berpikir logis, analitis, dan spasial siswa.
Komponen Utama dalam Soal Bangun Datar
Dalam mengerjakan soal-soal bangun datar, ada beberapa komponen penting yang perlu dipahami dan diperhatikan:
- Sisi: Garis lurus yang membentuk bangun datar.
- Titik Sudut: Titik pertemuan dua sisi.
- Sudut: Besaran putaran antara dua sisi yang bertemu pada titik sudut.
- Diagonal: Garis yang menghubungkan dua titik sudut yang tidak berdekatan.
- Keliling: Jarak total mengelilingi tepi luar dari bangun datar.
- Luas: Ukuran area yang dicakup oleh bangun datar.
Rumus-Rumus Dasar Bangun Datar
Setiap bangun datar memiliki rumus keliling dan luasnya masing-masing. Berikut adalah beberapa rumus dasar yang sering digunakan:
- Persegi:
- Keliling: $K = 4 times s$ (s = sisi)
- Luas: $L = s times s = s^2$
- Persegi Panjang:
- Keliling: $K = 2 times (p + l)$ (p = panjang, l = lebar)
- Luas: $L = p times l$
- Segitiga:
- Keliling: $K = a + b + c$ (a, b, c = panjang sisi-sisi segitiga)
- Luas: $L = frac12 times alas times tinggi$
- Lingkaran:
- Keliling: $K = 2 times pi times r$ atau $K = pi times d$ (r = jari-jari, d = diameter, $pi approx frac227$ atau 3.14)
- Luas: $L = pi times r^2$
Contoh Soal dan Pembahasan
Mari kita telaah beberapa contoh soal yang sering muncul di kelas 1 SMP beserta cara penyelesaiannya.
>
Soal 1: Persegi
Sebuah taman berbentuk persegi memiliki panjang sisi 15 meter. Hitunglah:
a. Keliling taman tersebut.
b. Luas taman tersebut.
Pembahasan:
Diketahui:
- Bentuk taman: Persegi
- Panjang sisi (s): 15 meter
Ditanya:
a. Keliling taman (K)
b. Luas taman (L)
Penyelesaian:
a. Menghitung Keliling:
Rumus keliling persegi adalah $K = 4 times s$.
Masukkan nilai sisi ke dalam rumus:
$K = 4 times 15$ meter
$K = 60$ meter
Jadi, keliling taman tersebut adalah 60 meter.
b. Menghitung Luas:
Rumus luas persegi adalah $L = s times s$ atau $L = s^2$.
Masukkan nilai sisi ke dalam rumus:
$L = 15 text meter times 15 text meter$
$L = 225 text meter^2$
Jadi, luas taman tersebut adalah 225 meter persegi.
>
Soal 2: Persegi Panjang
Sebuah papan tulis memiliki panjang 2 meter dan lebar 1.2 meter. Berapakah luas papan tulis tersebut?
Pembahasan:
Diketahui:
- Bentuk papan tulis: Persegi Panjang
- Panjang (p): 2 meter
- Lebar (l): 1.2 meter
Ditanya:
- Luas papan tulis (L)
Penyelesaian:
Rumus luas persegi panjang adalah $L = p times l$.
Masukkan nilai panjang dan lebar ke dalam rumus:
$L = 2 text meter times 1.2 text meter$
$L = 2.4 text meter^2$
Jadi, luas papan tulis tersebut adalah 2.4 meter persegi.
>
Soal 3: Segitiga
Sebuah segitiga memiliki alas sepanjang 20 cm dan tinggi 12 cm. Hitunglah luas segitiga tersebut.
Pembahasan:
Diketahui:
- Bentuk: Segitiga
- Alas: 20 cm
- Tinggi: 12 cm
Ditanya:
- Luas segitiga (L)
Penyelesaian:
Rumus luas segitiga adalah $L = frac12 times alas times tinggi$.
Masukkan nilai alas dan tinggi ke dalam rumus:
$L = frac12 times 20 text cm times 12 text cm$
$L = 10 text cm times 12 text cm$
$L = 120 text cm^2$
Jadi, luas segitiga tersebut adalah 120 cm persegi.
>
Soal 4: Lingkaran
Sebuah roda sepeda memiliki jari-jari 35 cm. Jika $pi$ diambil $frac227$, hitunglah keliling roda sepeda tersebut.
Pembahasan:
Diketahui:
- Bentuk: Lingkaran
- Jari-jari (r): 35 cm
- Nilai $pi$: $frac227$
Ditanya:
- Keliling roda (K)
Penyelesaian:
Rumus keliling lingkaran adalah $K = 2 times pi times r$.
Masukkan nilai jari-jari dan $pi$ ke dalam rumus:
$K = 2 times frac227 times 35 text cm$
$K = 2 times 22 times frac357 text cm$
$K = 2 times 22 times 5 text cm$
$K = 44 times 5 text cm$
$K = 220 text cm$
Jadi, keliling roda sepeda tersebut adalah 220 cm.
>
Soal 5: Kombinasi Bangun Datar
Perhatikan gambar berikut (bayangkan gambar sebuah rumah sederhana yang terdiri dari persegi dan segitiga di atasnya). Bagian utama rumah berbentuk persegi dengan panjang sisi 6 meter. Atap rumah berbentuk segitiga sama kaki dengan alas sama dengan panjang sisi persegi dan tinggi atap 4 meter. Hitunglah total luas bagian rumah tersebut (persegi dan atap segitiga).
Pembahasan:
Diketahui:
- Bagian rumah: Persegi dan Segitiga
- Sisi persegi: 6 meter
- Alas segitiga: 6 meter (sama dengan sisi persegi)
- Tinggi segitiga: 4 meter
Ditanya:
- Total luas bagian rumah (Luas Persegi + Luas Segitiga)
Penyelesaian:
-
Hitung Luas Persegi:
Rumus luas persegi: $Lpersegi = s times s$
$Lpersegi = 6 text meter times 6 text meter$
$L_persegi = 36 text meter^2$ -
Hitung Luas Segitiga:
Rumus luas segitiga: $Lsegitiga = frac12 times alas times tinggi$
$Lsegitiga = frac12 times 6 text meter times 4 text meter$
$Lsegitiga = 3 text meter times 4 text meter$
$Lsegitiga = 12 text meter^2$ -
Hitung Total Luas:
Total Luas = Luas Persegi + Luas Segitiga
Total Luas = $36 text meter^2 + 12 text meter^2$
Total Luas = $48 text meter^2$
Jadi, total luas bagian rumah tersebut adalah 48 meter persegi.
>
Soal 6: Mencari Sisi Jika Diketahui Luas (Persegi Panjang)
Sebuah lapangan bola voli memiliki luas 150 meter persegi. Jika panjang lapangan tersebut adalah 15 meter, berapakah lebar lapangan tersebut?
Pembahasan:
Diketahui:
- Bentuk: Persegi Panjang
- Luas (L): 150 meter persegi
- Panjang (p): 15 meter
Ditanya:
- Lebar lapangan (l)
Penyelesaian:
Rumus luas persegi panjang adalah $L = p times l$.
Untuk mencari lebar, kita bisa membagi luas dengan panjang: $l = fracLp$.
Masukkan nilai luas dan panjang ke dalam rumus:
$l = frac150 text meter^215 text meter$
$l = 10 text meter$
Jadi, lebar lapangan bola voli tersebut adalah 10 meter.
>
Tips Tambahan untuk Siswa:
- Pahami Konsep Dasar: Jangan hanya menghafal rumus, tetapi pahami dari mana rumus tersebut berasal dan bagaimana cara kerjanya.
- Buat Sketsa: Saat mengerjakan soal, terutama yang berkaitan dengan kombinasi bangun datar atau yang memiliki deskripsi, membuat sketsa sederhana dapat sangat membantu memvisualisasikan masalah.
- Perhatikan Satuan: Selalu perhatikan satuan yang digunakan dalam soal (misalnya meter, cm, km) dan pastikan satuan pada jawaban sesuai. Untuk luas, satuan akan selalu berbentuk kuadrat (misalnya meter persegi, cm persegi).
- Latihan Rutin: Semakin sering berlatih, semakin terbiasa siswa dalam mengenali pola soal dan menerapkan rumus yang tepat.
- Gunakan Kalkulator dengan Bijak: Untuk perhitungan yang rumit, kalkulator bisa membantu, namun pastikan siswa tetap memahami proses perhitungannya.
Kesimpulan
Mempelajari bangun datar adalah langkah awal yang penting dalam penguasaan matematika. Dengan memahami definisi, sifat-sifat, dan rumus-rumus dasar, siswa kelas 1 SMP dapat dengan percaya diri menjawab berbagai jenis soal. Contoh-contoh soal yang telah dibahas meliputi perhitungan keliling dan luas berbagai bangun datar, serta aplikasi dalam situasi nyata dan kombinasi bangun datar. Melalui latihan yang konsisten dan pemahaman konsep yang mendalam, siswa akan semakin mahir dalam menjelajahi dunia geometri.

Leave a Reply